Circa due settimane fa, ho letto questo post e poi quest’altro post del buon Juhan (blog da seguire, il suo) e niente, quando vedo qualche curiosità matematica, mi incanto come un bimbo (non sempre capisco tutto, ma ci provo).

E se c’è un linguaggio che ho studiato male all’Università, questo è OCaml. È allo stesso tempo però un linguaggio che mi ha sempre affascinato e sembra che non lo usi quasi nessuno, ma non è proprio così.

Dunque, riassumendo, il prodotto di Wallis è questo:

\[\begin{gather*} \prod_{n = 1}^{\infty} \left(\frac{4n^2}{4n^2 - 1}\right) = \prod_{n = 1}^{\infty} \left(\frac{2n}{2n-1} \cdot \frac{2n}{2n+1}\right) = \\ \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdots = \frac{\pi}{2} \end{gather*}\]

Per l’implementazione è sicuramente più pratica la forma compatta.

Ora come ora in OCaml sono una schiappa, ma non è stato difficile trovare una soluzione:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

(* calcola 4n^2 *)
let walp w =
  4. *. (w ** 2.)
;;

(* calcola il singolo termine della produttoria *)
let walt w =
	walp w /. (walp w -. 1.)
;;

(* Recursive Wallis *)
let wallis n =
	let rec wallis_rec i =
		if i = 1. then walt i else walt i *. wallis_rec(i -. 1.)
	in wallis_rec n
;;

Printf.printf "%.20f (Recursive)" (wallis (float_of_string Sys.argv.(1)));;
Printf.printf "\n1.5707963267948966192313216 (valore reale)\n\n";;

Printf.printf "%.20f (Recursive)" (2. *. wallis (float_of_string Sys.argv.(1)));;
Printf.printf "\n3.1415926535897932384626433 (valore reale)\n\n";;

Compilo con ocamlopt che produce codice nativo e lo mando in esecuzione:

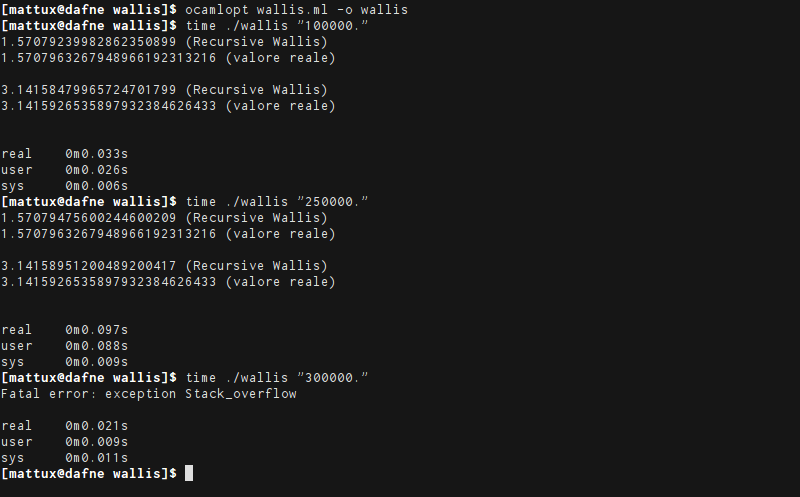
Recursive Wallis

Già dopo centomila iterazioni (lo so, non sono propriamente iterazioni) le prime cifre vengono approssimate bene, ma raggiunte le trecentomila, ottengo giustamente un bell’errore di stack overflow. Questo avviene perché la funzione non è tail recursive a causa delle operazioni aritmetiche tra le chiamate. Eliminiamole e riscriviamo la funzione:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

(* le funzioni walp e walt non cambiano *)

(* Tail Recursive Wallis *)
let wallis n =
	let rec wallis_tailrec n i =
		if n = 1. then i else  wallis_tailrec (n -. 1.) (i *. (walt n))
	in wallis_tailrec n (walt 1.)
;;

Printf.printf "%.20f (Tail Recursive)" (wallis (float_of_string Sys.argv.(1)));;
Printf.printf "\n1.5707963267948966192313216 (valore reale)\n\n";;

Printf.printf "%.20f (Tail Recursive)" (2. *. wallis (float_of_string Sys.argv.(1)));;
Printf.printf "\n3.1415926535897932384626433 (valore reale)\n\n";;

Ricompilo e mando in esecuzione:

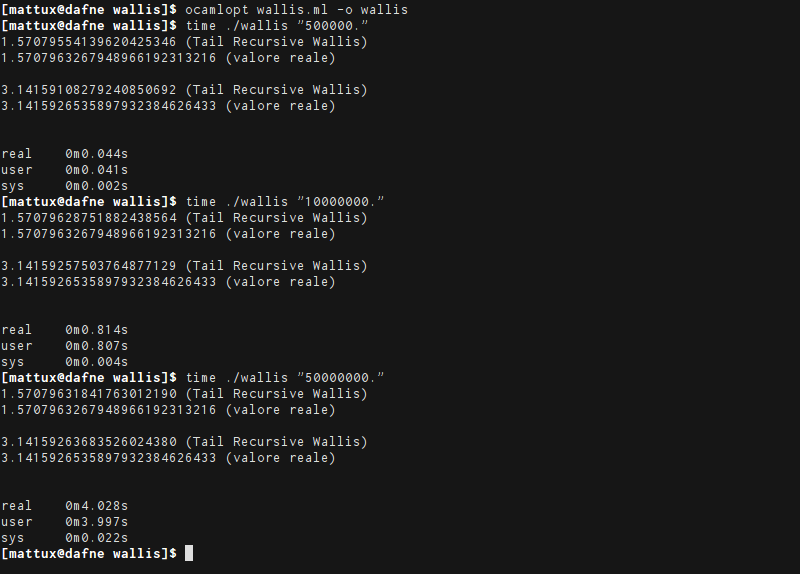
Tail Recursive Wallis

Molto, molto meglio. Addirittura riesce a fare 50 milioni di iterazioni (sostanzialmente ora lo sono per davvero) in 4 secondi.

Non so cosa volessi dimostrare con tutto ciò, però mi sono divertito.